一般要繪製ROC curve 除了要先具備基礎觀念
敏感度與特異度之外,並且知道ROC curve繪製過程,也就是變動閾值(threshold)獲得所有可能的敏感度與特異度,並將其收集為兩個變項軸x,y,其中的x軸為特異度(scentivity),y軸為1-特異度(1-specificity),並將其做圖,就是建立ROC曲線圖.
如下圖:
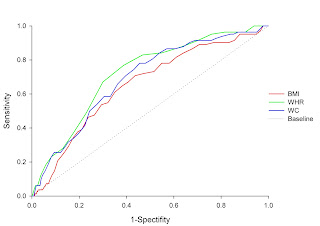
然而要利用SAS計算並且繪製似乎在SAS程式內未提供詳細說明與做法,吾在此提供兩種方法,在繪製前提尚需了解SAS如何處理資料,當欲考量兩族群(y=1or0)在自變數(x)的變化下對於該自變數能否有效鑑別出兩族群,一般而言會考量使用Logistic regression方法,以下為Logistic regression機率函數

並針對兩族群對於自變項設定model如下

此為Logistic regression 方程式模式化Modeling,並且SAS係利用反應變數x轉換為預測機率值將其計算該模式的特異度(scentivity),1-特異度(1-specificity)在將其繪製,自變項與預測機率關係是一對一
PROC logistic descending ;
MODEL y = x / OUTROC=roc;
output out=pred xbeta=x p=p;
RUN;
|
接著就是如何利用這樣的結果資料輸出為圖形,吾蒐集資料後提供吾所知道的方法,方法如下
計算與繪製:1.
ODS語法:此為SAS內建ODS語法
2.
Nonparametric comparison of areas under correlated ROC curves:此為SAS macro語法,由SAS support,用來針對變項做計算與比較
3.
Plot ROC curve with labelled points for a binary-response model:此為SAS macro語法,由SAS support,用來繪製ROC curve圖形,可與上述語法並用
4.
簡易應用:將macro語法簡化使用
1.
ODS語法ODS html;
ODS graphics ON;
PROC logistic descending ;
MODEL y = x / OUTROC=roc;
RUN;
ODS graphics off;
ODS html CLOSE;
|
此方法是利用SAS內建ODS輸出語法將計算後的預測機率報表中的ROC資料加以繪製圖形,但此方法能力還是有限,僅能提供單一曲線以及該曲線的面積(AUC)
2.
Nonparametric comparison of areas under correlated ROC curves | |
%roc(DATA= , VAR= , RESPONSE= , CONTRAST= , ALPHA= , DETAILS= ) ;
|
此方法為SAS提供的巨集語法macro,此語法特性是先將以下巨集語法先讀入,在設定上述語法方能計算出該資料的兩族群與自變項的曲線下面積(AUC)與該曲線95%C.I.,此法優點在於可比較多組自變項在兩族群間的效用並做檢定
巨集語法%roc
%macro roc(version, data=, var=, response=, contrast=, details=no,
alpha=.05);
%let _version=1.6;
%if &version ne %then %put ROC macro Version &_version;
%let opts = %sysfunc(getoption(notes))
_last_=%sysfunc(getoption(_last_));
options nonotes;
/* Check for newer version */
%if %sysevalf(&sysver >= 8.2) %then %do;
filename _ver url 'http://ftp.sas.com/techsup/download/stat/versions.dat' termstr=crlf;
data _null_;
infile _ver;
input name:$15. ver;
if upcase(name)="&sysmacroname" then call symput("_newver",ver);
run;
%if &syserr ne 0 %then
%put ROC: Unable to check for newer version;
%else %if %sysevalf(&_newver > &_version) %then %do;
%put ROC: A newer version of the ROC macro is available.;
%put %str( ) You can get the newer version at this location:;
%put %str( ) http://support.sas.com/ctx/samples/index.jsp;
%end;
%end;
title "The ROC Macro";
title2 " ";
%let error=0;
/* Verify that DATA= option is specified */
%if &data= %then %do;
%put ERROR: Specify DATA= containing the OUT= data sets of models to be compared;
%goto exit;
%end;
/* Verify that VAR= option is specified */
%if &var= %then %do;
%put ERROR: Specify predictor or XBETA variables in the VAR= argument;
%goto exit;
%end;
/* Verify that RESPONSE= option is specified */
%if &response= %then %do;
%put ERROR: Specify response variable in the RESPONSE= argument;
%goto exit;
%end;
%let i=1;
%do %while (%scan(&data,&i) ne %str() );
%let data&i=%scan(&data,&i);
%let i=%eval(&i+1);
%end;
%let ndata=%eval(&i-1);
data _comp(keep = &var &response);
%if &data=%str() or &ndata=1 %then set;
%else merge;
&data;
if &response not in (0,1) then call symput('error',1);
run;
%if &error=1 %then %do;
%put ERROR: Response must have values 0 or 1 only.;
%goto exit;
%end;
/* Original SAS/IML code from author follows */
proc iml;
start mwcomp(psi,z);
*;
* program to compute the mann-whitney components ;
* z is (nn by 2);
* z[,1] is the column of data values;
* z[,2] is the column of indicator variables;
* z[i,2]=1 if the observation is from the x population;
* z[i,2]=0 if the observation is from the y population;
*
* psi is the returned vector of u-statistic components;
rz = ranktie( z[,1] ); * average ranks;
nx = sum( z[,2] ); * num. of Xs ;
ny = nrow(z)-nx; * num of Ys ;
loc = loc( z[,2]=1 ); * x indexes ;
psi = j(nrow(z),1,0);
psi[loc] = (rz[loc] - ranktie(z[loc,1]))/ny; * x components ;
loc = loc( z[,2]=0 ); * y indexes ;
psi[loc] = ( nx+ranktie(z[loc,1])-rz[loc])/nx; * y components ;
free rz loc nx ny; * free space ;
finish;
start mwvar(t,v,nx,ny,z);
*;
* compute mann-whitney statistics and variance;
* input z, n by (k+1);
* z[,1:k] are the different variables;
* z[,k+1] are indicator values,
* 1 if the observation is from population x and ;
* 0 if the observation is from population y;
* t is the k by k vector of estimated statistics;
* the (i,j) entry is the MannWhitney statistic for the
* i-th column when used with the j-th column. The only
* observations with nonmissing values in each column are
* used. The diagonal elements are, hence, based only on the
* single column of values.
* v is the k by k estimated variance matrix;
* nx is the matrix of x population counts on a pairwise basis;
* ny is the matrix of y population counts on a pairwise basis;
k = ncol(z)-1;
ind = z[,k+1];
v = j(k,k,0); t=v; nx=v; ny=v;
* The following computes components after pairwise deletion of
* observations with missing values. If either there are no missing
* values or it is desired to use the components without doing
* pairwise deletion first, the nested do loops could be evaded.
*;
do i=1 to k;
do j=1 to i;
who = loc( (z[,i]^=.)#(z[,j]^=.) ); * nonmissing pairs;
run mwcomp(psii,(z[,i]ind)[who,]); * components;
run mwcomp(psij,(z[,j]ind)[who,]);
inow = ind[who,]; * Xs and Ys;
m = inow[+]; * current Xs;
n = nrow(psii)-m; * current Ys;
nx[i,j] = m; ny[i,j] = n;
mi = (psii#inow)[+] / m; * means;
mj = (psij#inow)[+] / m;
t[i,j] = mi; t[j,i] = mj;
psii = psii-mi; psij = psij-mj; * center;
v[i,j] = (psii#psij#inow)[+] / (m#(m-1))
+ (psii#psij#(1-inow))[+] / (n#(n-1));
v[j,i] = v[i,j];
end;
end;
free psii psij inow ind who;
finish;
/* start of execution of the IML program */
use _comp var {&var &response};
read all into data [colname=names];
run mwvar(t,v,nx,ny,data); * estimates and variances;
vname = names[1:(ncol(names)-1)];
manwhit = vecdiag(t);
/* omit: 0 for intercept-only model; not needed for further
computations
c=sqrt( vecdiag(v) ); c=v / (c@c`);
%if %upcase(%substr(&details,1,1)) ne N %then %do;
print c [label='Estimated Correlations' colname=vname rowname=vname];
%end;
*/
%if &contrast= %then %do;
%put ROC: No contrast specified. Pairwise contrasts of all;
%put %str( ) curves will be generated.;
call symput('col',char(ncol(data)-1));
%if &col=1 %then %str(l=1;); %else %do;
l=(j(&col-1,1)-i(&col-1))
%do i=&col-2 %to 1 %by -1;
//(j(&i,&col-&i-1,0)j(&i,1)-i(&i))
%end;
;
%end;
%end;
%else %do;
l = { &contrast };
%end;
lt=l*manwhit;
lv=l*v*l`;
c = ginv(lv);
chisq = lt`*c*lt;
df = trace(c*lv);
p = 1 - probchi( chisq, df );
/* Original SAS/IML code by author ends */
/* Individual area stderrs and CIs */
stderr=sqrt(vecdiag(v));
arealcl=manwhit-probit(1-&alpha/2)*stderr;
areaucl=manwhit+probit(1-&alpha/2)*stderr;
areastab=putn(manwhitstderrarealclareaucl,'7.4');
/* Pairwise difference stderrs and CIs */
sediff=sqrt(vecdiag(lv));
difflcl=lt-probit(1-&alpha/2)*sediff;
diffucl=lt+probit(1-&alpha/2)*sediff;
diffchi=(lt##2)/vecdiag(lv);
diffp=1-probchi(diffchi,1);
%if %upcase(%substr(&details,1,1)) ne N %then %do;
print t [label='Pairwise Deletion Mann-Whitney Statistics' colname=vname
rowname=vname];
%end;
print areastab [label=
"ROC Curve Areas and %sysevalf(100*(1-&alpha))% Confidence Intervals"
rowname=vname colname={'ROC Area' 'Std Error' 'Confidence' 'Limits'}];
call symput('maxrow',char(comb(max(nrow(l),2),2)));
rname='Row1':"Row&maxrow";
%if %upcase(%substr(&details,1,1)) ne N %then %do;
print v [label='Estimated Variance Matrix' colname=vname rowname=vname];
print nx [label='X populations sample sizes' colname=vname rowname=vname];
print ny [label='Y populations sample sizes' colname=vname rowname=vname];
print lv [label='Variance Estimates of Contrast' rowname=rname
colname=rname];
%end;
print l [label='Contrast Coefficients' rowname=rname colname=vname];
fdiffchi=putn(diffchi,'9.4');
fdiffp=putn(diffp,'pvalue.');
diffs=putn(ltsediffdifflcldiffucl,'7.4');
diffstab=diffsfdiffchifdiffp;
print diffstab [label=
"Tests and %sysevalf(100*(1-&alpha))% Confidence Intervals for Contrast Rows"
rowname=rname colname={'Estimate' 'Std Error' 'Confidence' 'Limits'
'Chi-square' 'Pr > ChiSq'}];
c2=putn(chisq,'9.4');
df2=putn(df,'3.');
p2=putn(p,'pvalue.');
ctest=c2df2p2;
print ctest [label='Contrast Test Results'
colname={'Chi-Square' ' DF' 'Pr > ChiSq'}];
/* Make overall p-value available */
%global pvalue;
call symput('pvalue',p2);
quit;
%exit:
options &opts;
title; title2;
%mend;
3.
Plot ROC curve with labelled points for a binary-response model%rocplot(out= , outroc= , p= , id= , plottype= , roffset= , font= , size= , color= , position= , plotchar= );
|
此方法為SAS提供的巨集語法macro,此語法特性是先將以下巨集語法先讀入,在設定上述語法方能繪出該自變項與兩族群間的ROC曲線,另外也能同時繪製多個自變項在同一張圖層上,並也能配合方法二
巨集語法%rocplot
%macro rocplot ( version, outroc=, out=, p=, id=, plottype=high, font=swissb,
size=2, position=F, color=black, plotchar=dot,
roffset=4, round=1e-8 );
%if &version ne %then %put ROCPLOT macro Version 1.0;
options nonotes;
%let nomatch=0;
/* Verify ID= is specified */
%if %quote(&id)= %then %do;
%put ERROR: The ID= option is required.;
%goto exit;
%end;
/* Verify P= is specified */
%if %quote(&p)= %then %do;
%put ERROR: The P= option is required.;
%goto exit;
%end;
/* Verify OUTROC= is specified and the data set exists */
%if %quote(&outroc) ne %then %do;
%if %sysfunc(exist(&outroc)) ne 1 %then %do;
%put ERROR: OUTROC= data set not found.;
%goto exit;
%end;
%end;
%else %do;
%put ERROR: The OUTROC= option is required.;
%goto exit;
%end;
/* Verify OUT= is specified and the data set exists */
%if %quote(&out) ne %then %do;
%if %sysfunc(exist(&out)) ne 1 %then %do;
%put ERROR: OUT= data set not found.;
%goto exit;
%end;
%end;
%else %do;
%put ERROR: The OUT= option is required.;
%goto exit;
%end;
data _outroc;
set &outroc;
_prob_=round(_prob_,&round);
run;
data _out;
set &out;
_prob_=round(&p , &round);
length _id $ 200;
/* Create single label variable */
_id=trim(left(%scan(&id,1)))
%let i=2;
%do %while (%scan(&id,&i) ne %str() );
'/'trim(left(%scan(&id,&i)))
%let i=%eval(&i+1);
%end;
;
run;
proc sort data=_out nodupkey;
by _prob_ _id;
run;
proc sort data=_outroc nodupkey;
by _prob_;
run;
data _rocplot;
_inout=0; _inroc=0;
merge _outroc(in=_inroc) _out(in=_inout);
by _prob_;
if not(_inout and _inroc) then do;
call symput('nomatch',1);
delete;
end;
run;
%if &nomatch=1 %then %do;
%put ROCPLOT: Some predicted values in OUT= did not match predicted values;
%put %str( in OUTROC=. Verify that you used the ROCEPS=0 option in);
%put %str( PROC LOGISTIC.);
%end;
%if %upcase(%substr(&plottype,1,1))=L %then %do;
footnote "Point labels are values of &id";
proc plot data=_rocplot;
plot _sensit_*_1mspec_ $ _id /
haxis=0 to 1 by .1 vaxis=0 to 1 by .1;
run; quit;
%end;
%if %upcase(%substr(&plottype,1,1))=H %then %do;
data _anno;
length function style color $ 8 position $ 1 text $ 200;
retain function 'label' xsys ysys '2' hsys '3'
size &size position "&position" style "&font"
color "&color";
set _rocplot(keep=_sensit_ _1mspec_ _id) end=eof;
x=_1mspec_; y=_sensit_; text=trim(left(_id)); output;
/* Draw (0,0) to (1,1) reference line */
if eof then do;
x=0; y=0; function='move'; output;
x=1; y=1; function='draw'; line=1; hsys='1'; size=0.25; output;
end;
run;
symbol1 i=join v=&plotchar c=blue l=1;
footnote "Point labels are values of &id";
axis1 offset=(1,&roffset)pct order=(0 to 1 by .1);
proc gplot data=_rocplot;
plot _sensit_*_1mspec_=1 / vaxis=0 to 1 by .1
haxis=axis1 annotate=_anno;
run;
quit;
%end;
footnote;
%exit:
options notes;
%mend;
4.
簡易應用吾將語法簡化使用方式如下:
利用方法1可以簡單快速計算與繪製,也可獨立使用方法2與3
PROC logistic descending ;
MODEL y = x / OUTROC=roc;
output out=pred xbeta=x p=p;
RUN;
|
上述為前置動作是將依變項y與自變項x先計算出預測機率
接著先將方法2與3的巨集語法先讀入在執行下述語法
曲線下面積(AUC):
%roc(DATA=pred , VAR=p , RESPONSE=y );
ROC曲線圖:
%rocplot(out=pred , outroc=roc , p=p , id=x , color=white );
|
利用巨集語法計算曲線下面積(AUC)的計算也可略過Logisitc regression分析直接計算
曲線下面積(AUC):
%roc(DATA=資料 , VAR=自變項 , RESPONSE=兩族群(1,0) );
此用法前提為無遺漏值
|
References
SAS support
1.
Nonparametric comparison of areas under correlated ROC curves2.
Plot ROC curve with labelled points for a binary-response modelWikipedia
Receiver operating characteristic












